Loop the loop met een auto

Als je voldoende geld en middelen hebt kan je fysica erg aantrekkelijk maken.
Ik herinner mij hoe ik destijds bij de bespreking van de cirkelvormige beweging ook de looping aan bod liet komen.
Mijn didactisch materiaal bestond uit bord en krijt en een setje met een met een paar metalen kogels, zoals op volgende foto. Meer niet.

 
De mannen van het Engelse TV-station Five.TV daarentegen, kunnen zich, ondanks alle crisissen, permitteren om zo’n looping echt te bouwen.
In het groot dan nog wel: een loop met 6,5 m straal! En daar laten ze dan geen stalen kogeltjes op racen, maar een echte auto!
In het filmpje verderop zie je hoe ze dat in een uitzending van hun automagazine Fifth Gear met veel show inkleden en presenteren.

Maar toch eerst een klein beetje fysica.
Want rond een cirkelbeweging bestaan er teveel misvattingen en die wil ik uit de wereld helpen.
Om een voorwerp een cirkelbeweging te laten maken is er op het voorwerp ALLEEN een kracht naar het middelpunt nodig. ALLEEN een middelpuntzoekende kracht of centripetale kracht.
Op het voorwerp is er dus helemaal geen sprake van een kracht naar buiten toe, van het middelpunt weg. Helemaal GEEN middelpuntvliedende kracht dus. Helemaal geen centrifugale kracht!
Het optreden van een middelpuntvliedende kracht is misvatting die maar blijft voortbestaan. Sommigen blijven daarin geloven.
Maar bedenk b.v. dat als je een steen aan een touw wil laten rondzwieren, je voortdurend, via de koord, de steen naar het midden moet trekken. Oefen je die kracht naar het midden niet uit (als je de koord loslaat b.v.) dan beschrijft de steen geen cirkel meer. Hij gaat rechtdoor en begint te vallen onder invloed van de zwaartekracht.

Bij de steen aan een koord is het dus de trekkracht via het touw die voor de kracht naar het middelpunt zorgt.
Maar wat zorgt voor die kracht op het voorwerp bij een looping?
Laten we dat eens bekijken in het cruciale punt: het hoogste punt van de looping.
 
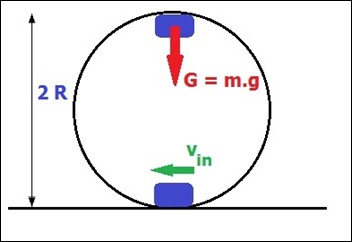
De enige kracht die daar op het voorwerp werkt is de zwaartekracht, dus het gewicht G van het voorwerp.
En misschien weten jullie nog wel uit jullie schooltijd dat het gewicht van een voorwerp gelijk is aan zijn massa maal de valversnelling g. Dus G = m.g
En Newton heeft in de 17de eeuw al aangetoond dat bij elke cirkelbeweging de centripetale kracht = m.v²/R
Jullie moeten dat dus maar geloven.
Dat betekent dus dat m.g = m.v²/R
Daaruit kunnen we de minimale snelheid v berekenen die het voorwerp in de top moet hebben om een cirkel te kunnen beschrijven:

In het filmpje hieronder is R = 6,5 m. Als je weet dat g ≈10 m/s² dan kan je berekenen dat de minimale snelheid van de auto in het hoogste punt v = 8 m/s moet zijn of 29 km/h.
Maar dan moet de snelheid v_in van de auto bij het binnenkomen van de loop natuurlijk een stuk groter zijn, want de auto moet nog over een hoogte 2R stijgen!
Het is te berekenen (maar ik laat dat hier achterwege) dat
v_in ≈ 58 km/h.
Die snelheid mag ook niet hoger zijn, want dan zou de constructie het begeven.

Ik hoop maar dat dit niet van het goede teveel was, en dat jullie nog kunnen genieten van het stuntwerk en de show.
En wil je nog meer gegevens over het hele experiment, dan kan je eens een kijkje nemen op een site van Dunlop, die het hele gebeuren gesponsord heeft.